How does a reasoner work?

Summary

Reasoners should play a vital role in developing and using an ontology written in OWL. Automated reasoners such as Pellet, FaCT++, HerMiT, ELK and so on take a collection of axioms written in OWL and offer a set of operations on the ontology’s axioms – the most noticeable of which from a developer’s perspective is the inference of a subsumption hierarchy for the classes described in the ontology. A reasoner does a whole lot more and in this kblog we will examine what actually goes on inside a DL reasoner, what is offered by the OWL API and then what is offered in an environment like Protégé.

authors

Uli Sattler and Robert Stevens
Information Management BioHealth Informatics Groups
School of Computer Science
University of Manchester
Oxford Road
Manchester
United Kingdom
M13 9PL
Ulrike.Sattler@Manchester.ac.uk and robert.stevens@Manchester.ac.uk

Phillip Lord
School of Computing Science
Newcastle University+ Newcastle
United Kingdom
NE3 7RU
phillip.lord@newcastle.ac.uk

What a reasoner does

One of the most widely known usages of the reasoner is classification – we will first explain what this is, and then sketch other things a reasoner does. There are other (reasoning) services that a reasoner can carry out, such as query answering, but classification is the service that is invoked, for example, when you click “Start Reasoner” in the Protégé 4 ontology editor.

So, assume you have loaded an ontology O (which includes resolving its imports statements and parsing the contents of all relevant OWL files) and determined the axioms in O – then you also know all the class names that occur in axioms in O: let’s call this set N (for names). When asked to classify O, a reasoner does the following three tasks:

First, it checks whether there exists a model (http://ontogenesis.knowledgeblog.org/55) of O, that is, whether there exists a (relational) structure that satisfies (http://ontogenesis.knowledgeblog.org/1329) all axioms in O. For example, the following ontology would fail this test since Bob cannot be an instance of two classes that are said to be disjoint, i.e., each structure would have to violate at least one of these three axioms:

 Class: Human
 Class: Sponge
 Individual: Bob types: Sponge
 Individual: Bob types: Human
 DisjointClasses: Human, Sponge

In case this test is failed, the reasoner returns a warning “this ontology is inconsistent (http://ontogenesis.knowledgeblog.org/1329) ” which is handled differently in different tools. In case this test is passed, the classification process continues to the next step.

Second, for each class name that occurs in O – i.e., for each element A in N, the reasoner tests whether there exists a model of O in which we find an instance x of A, i.e., whether there exists a (relational) structure that satisfies all the axioms in O and in which A has an instance, say x. For example, the following ontology would pass the first “consistency” test, but still would fail this “satisfiability” (http://ontogenesis.knowledgeblog.org/1329) test for A (while passing it for the other class names, namely Human and Sponge):

 Class: Human
 Class: Sponge
 DisjointClasses: Human, Sponge
 Class: A SubClassOf: (likes some (Human and Sponge))

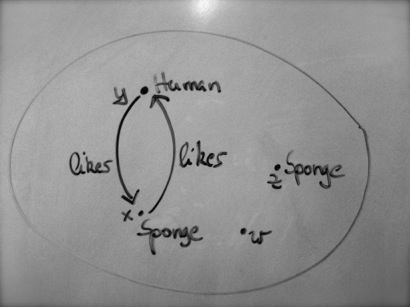
The picture above shows a model of this ontology with x and z being instances of Sponge, y being an instance of Human, and x and y liking each other. Classes that fail this satisfiability test are marked by Protégé in red in the inferred class hierarchy, and the OWL API has them as subclasses of owl:Nothing.

Thirdly, for any two class names, say A and B, that occur in O, the reasoner tests whether A is subsumed by B, i.e., whether in each model of O, each instance of A is also an instance of B. In other words, whether in each (relational) structure that satisfies all axioms in O, every instance of SBL is also one of SL. For example, in the ontology below (where Sponge and Human are no longer disjoint), DL is subsumed by SBL which, in turn, is subsumed by AL.

 Class: Animal
 Class: Human SubClassOf: Animal
 Class: Sponge SubClassOf: Animal
 Class: SBL EquivalentTo: (likes some (Human and Sponge))
 Class: AL  EquivalentTo: (likes some Animal)
 Class: DL SubClassOf: (likes some Human) and (likes only Sponge)

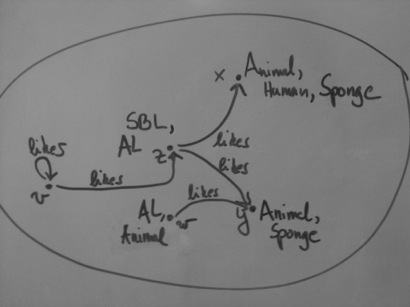
The picture above shows a model of this ontology with, for example, x being an insance of Sponge, Human, and Animal, and z being an instance of SBL and AL.

The results of these subsumption tests are shown in the Protégé OWL editor in the form of the inferred class hierarchy, where classes can appear deeper than in the (told) class hierarchy.

Alternatively, we can describe the classification service also in terms of entailments: a reasoner determines all entailments of the form

A SubClassOf B

of a given ontology, where

• A is owl:Thing and B is owl:Nothing – this is the consistency test, or
• A is a name and B is owl:Nothing – these are the satisfiability tests, or
• A and B are either class names in the ontology – these are the subsumption tests.

When we talk about a “reasoner”, we understand that it is sound, complete, and terminating: i.e., all entailments it finds do indeed hold, it finds all entailments that hold, and it always stops eventually. If a “inference engine” relies on an algorithm that is not sound or complete or terminating, we would not usually call it a reasoner.

Other things we can ask a reasoner to do is to retrieve instances, subclasses, or superclasses of a given, anonymous class expression, or to answer a conjunctive query.

How a reasoner works

These days, we usually distinguish between consequence-driven reasoning and tableau-based approaches to reasoning, and both are available in highly optimised implementations, i.e., reasoners.

Consequence-driven approaches have been shown to be very efficient for so-called Horn fragments of OWL
[A Horn fragment is one that excludes any form of disjunction, i.e., we cannot use “or” in class expressions, or (not (A and B)), or other constructs that require some form of reasoning by case.]
. In a nutshell, given an ontology O, they apply deduction rules (not to be confused with those in rule-based systems or logic programs) to infer entailments from O and other axioms that have already been inferred. For example, one of these deduction rules would infer

M SubClassOf (p some B)

from

A SubClassOf: B
M SubClassOf (p some A)

For example, ELK employs such a consequence-driven approach for the OWL 2 EL profile.

Tableau-based reasoners have been developed for more expressive logics, e.g., Fact++, Pellet, Racer, Konclude. As you can see, the first 2 tests (consistency and satisfiability) ask for a (!) model of the ontology – where a given class name has an instance, for the satisfiability test. And a tableau-based reasoner tries to construct such a model using so-called completion rules that work on (an abstraction of) such a model, trying to extend it so that it satisfies all the axioms. For example, assume it is started with the following ontology and asked whether DL is satisfiable in it:

 Class: Animal SubClassOf: (hasParent some Animal)
 Class: Human SubClassOf: Animal
 Class: Sponge SubClassOf: Animal
 Class: SBL EquivalentTo: Animal and (likes some (Human and Sponge))
 Class: AL  EquivalentTo: Animal and  (likes some Animal)
 Class: DL SubClassOf: Animal and  (likes some Human) and (likes only Sponge)

The reasoner will try to generate a model with an instance x of DL. Because of the last axiom, a completion rule will determine that x also needs to be an instance of

 Animal and  (likes some Human) and (likes only Sponge)

A so-called “and” completion rule will take this class expression apart and will explicate that x has to be an instance of DL (from the start), Animal, (likes some Human), and (likes only Sponge). Yet another rule, the “some” rule, will generate another individual, say y, as a likes-filler of x and makes y an instance of Human. Now various other rules are applicable: the “only” rule can add the fact that y is an instance of Sponge because y is likes-related to x and x is an instance of (likes only Sponge). The “is-a” rule can spot that y is an instance of Animal (because it is an instance of Human and the second axiom). And we can also have the “some” rule add a hasParent-filler of x, say z, and make z an Animal to satisfy the first axiom. We would also need to do a similar thing to y since y also is an Animal.

In this way, completion rule “spot” constraints imposed by axioms on a model, and thereby build a model that satisfies our ontology. Two things make this a rather complex task: firstly, we can’t continue creating hasParent-fillers of Animal because then we wouldn’t terminate. That is, we have to stop this process while making sure that the result is still a model. This is done by a cycle-detection mechanism called “blocking” (see Baader and Sattler paper at the end of this kblog). Secondly, our ontology didn’t involve a disjunction: if we were to add the following axiom

Class: Human SubClassOf: Child or Adult

then we would need to guess whether y is a Child or an Adult. In our example, both guesses are ok – but in a more general setting our first guess may fail (i.e., lead to an obvious contradiction like y is an instance of 2 disjoint classes) and we would have to backtrack.

So, in summary, our tableau algorithm tries to build a model of the ontology by applying completion rules to the individuals in that model – possibly generating new ones – to ensure that all of them (and their relations) satisfy all axioms in the ontology. For an inconsistent ontology (http://ontogenesis.knowledgeblog.org/1329) (or a consistent one where we try to create an instance of an unsatisfiable class), this attempt will fail with an obvious “clash”, i.e., an obvious contradiction like an individual being an instance of 2 disjoint classes. And it will succeed otherwise with (an abstraction of) a model. For a subsumption test to decide whether A is subsumed by B, we try to build a model with an instance of A and not (B): if this fails, then A and not(B) cannot have an instance in any model of the ontology, hence A is subsumed by B!

Last words

We have tried to describe what reasoners do, and how they do this. Of course, this explanation had to be high-level and leave out a lot of detail, and we had to concentrate on the classification reasoning service and thus didn’t really mention other ones such as query answering. Moreover, a lot of interaction with a reasoner is currently being realised via the OWL API, and we haven’t mentioned this at all.

To be at least complete in some aspect, we would like to leave you with the following links:

• List of OWL reasoners
• List of reasoners (curated at Manchester)

Some helpful web sites:

• OWL-2 primer
• OWL Reasoning Examples

The paper by Franz Baader and Ulrike Sattler (10.1023/A:1013882326814) will be useful.

Bibliography